The Coven-Meyerowitz conjecture is a tentative characterization of finite sets that tile the integers by translations. It’s also something I have been thinking about, on and off, for more than 2 decades; in the last few years, Itay Londner and I were finally able to make some progress on it. This post will provide a short introduction to the problem, some history, and a little bit of speculation. In a follow-up post (or posts, as there might be more than one), I will say more about our recent work.
The basics. Let  be a set of integers; in this series of posts, we will always assume that
be a set of integers; in this series of posts, we will always assume that  is finite. We will say that
is finite. We will say that  tiles
tiles 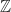 by translations if
by translations if 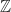 can be covered by non-overlapping translated copies of $\latex A$. We will use
can be covered by non-overlapping translated copies of $\latex A$. We will use 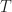 to denote the set of translations. For example:
to denote the set of translations. For example:
- The set
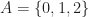 tiles
tiles 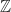 by translations. Indeed, we can just place copies of
by translations. Indeed, we can just place copies of  next to each other, back to back. A possible translation set is
next to each other, back to back. A possible translation set is  . Note that the translation set need not be unique: for example,
. Note that the translation set need not be unique: for example,  would also work in this case.
would also work in this case.
- The set
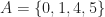 also tiles
also tiles 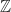 by translations. For example, we can add its translate
by translations. For example, we can add its translate 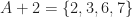 to fill up the discrete interval
to fill up the discrete interval  , then continue the pattern.
, then continue the pattern.
- The set
 does not tile
does not tile 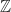 by translations. Once
by translations. Once  is in place, there is no way to add a second translate
is in place, there is no way to add a second translate 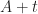 , non-overlapping with
, non-overlapping with  , so that
, so that 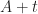 would cover the point 1. (Try it!)
would cover the point 1. (Try it!)
In the above examples, it’s easy to tell whether each set does or does not tile the integers. However, suppose that  is a set of 30 integers between 0 and 100,000. What then? How can we tell whether
is a set of 30 integers between 0 and 100,000. What then? How can we tell whether  tiles the integers or not?
tiles the integers or not?
Read more: The Coven-Meyerowitz conjecture
A periodicity argument due to Newman says that the question is decidable, meaning that there is a guaranteed way to get a “yes” or “no” answer in finite time. Specifically, Newman proved the following theorem.
Theorem (Newman). Let  be finite. If
be finite. If  tiles the integers, then every such tiling is periodic with period bounded by
tiles the integers, then every such tiling is periodic with period bounded by  .
.
Here’s the idea of the proof: if  tiles the integers, then it must also tile a discrete interval of length
tiles the integers, then it must also tile a discrete interval of length  . Once it does that, there is only one way to continue the tiling in each direction, and because there are only finitely many configurations of that length available, at some point they have to start repeating themselves, making the tiling periodic. Do this carefully, and you get Newman’s theorem.
. Once it does that, there is only one way to continue the tiling in each direction, and because there are only finitely many configurations of that length available, at some point they have to start repeating themselves, making the tiling periodic. Do this carefully, and you get Newman’s theorem.
Let’s say, then, that 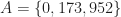 . How can we tell whether
. How can we tell whether  tiles the integers? As per the above, we expect the tiling to have period at most
tiles the integers? As per the above, we expect the tiling to have period at most  . We could have a computer check all arrangements of translates of
. We could have a computer check all arrangements of translates of  by shifts between
by shifts between  and
and  , and if we do not find a tiling of period bounded by that number, then none exists.
, and if we do not find a tiling of period bounded by that number, then none exists.
Fortunately, in this case we could also do something more clever than using brute force. Notice that  is a full set of residues modulo
is a full set of residues modulo 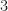 , with
, with 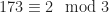 and
and 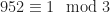 . Therefore
. Therefore  actually tiles the integers with tiling period 3 and the translation set
actually tiles the integers with tiling period 3 and the translation set 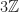 .
.
How did I know to check the residues mod 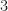 ? Is there a way to do such “smart tricks” more systematically? Also, does this mean that
? Is there a way to do such “smart tricks” more systematically? Also, does this mean that 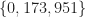 does not tile the integers?
does not tile the integers?
Let’s see.
The polynomial formulation. Let  tile the integers with period
tile the integers with period 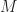 . This means that the translation set
. This means that the translation set 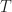 has period
has period 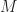 . so that
. so that 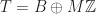 for some finite
for some finite 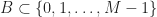 . Reducing mod
. Reducing mod 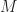 , we may also assume that
, we may also assume that 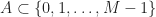 , and write
, and write  .
.
(A word on notation: we write 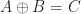 to say that for every
to say that for every 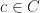 there is a unique pair
there is a unique pair  such that
such that 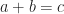 . We use
. We use 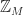 to denote
to denote 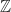 modulo
modulo 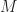 . From now on, we will always consider
. From now on, we will always consider 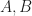 as subsets of
as subsets of 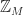 , with addition mod
, with addition mod 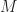 .)
.)
We now introduce the polynomial notation. We will use 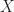 to denote a variable, and define the mask polynomials
to denote a variable, and define the mask polynomials
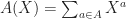 ,
,  .
.
(Note that 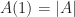 , the cardinality of
, the cardinality of  .) Then the tiling condition
.) Then the tiling condition  is equivalent to
is equivalent to
(1) 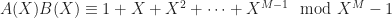 .
.
This reformulation of the problem is easy (just multiply out the product and compare the exponents), but very useful, because now we can use factorization of polynomials.
Cyclotomic polynomials. The  -th cyclotomic polynomial
-th cyclotomic polynomial 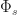 is the unique irreducible monic polynomial whose roots are the
is the unique irreducible monic polynomial whose roots are the  -th primitive roots of unity. An alternative definition that will be useful to us is based on factorization: for all
-th primitive roots of unity. An alternative definition that will be useful to us is based on factorization: for all 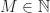 , we have
, we have
(2) 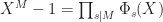 ,
,
and this can be used to define all 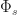 inductively. (Here and below, we always consider only the positive divisors, so that
inductively. (Here and below, we always consider only the positive divisors, so that  .) Start with
.) Start with
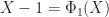 ,
,
because clearly 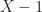 is irreducible and the only divisor of 1 is 1. Next,
is irreducible and the only divisor of 1 is 1. Next,
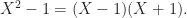
Since we have already established that 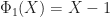 , it follows that
, it follows that 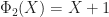 . Similarly,
. Similarly,
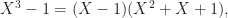
so that 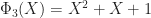 . This is part of a more general pattern: if
. This is part of a more general pattern: if 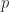 is a prime number, then by the same argument we have
is a prime number, then by the same argument we have 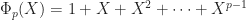 . Furthermore, if
. Furthermore, if 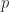 is prime and
is prime and 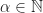 , we can write
, we can write
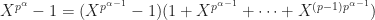
so that by induction,
(3) 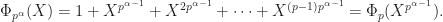
For a composite example, let’s compute 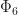 :
:
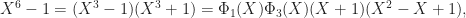
where we used that 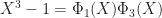 as above. Also, we already know that
as above. Also, we already know that 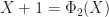 , so that leaves
, so that leaves 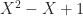 as
as 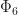 .
.
The Coven-Meyerowitz tiling conditions. Coming back to the tiling equation (1), we see that each 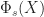 with
with 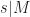 and
and 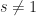 must divide
must divide 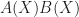 . Since
. Since 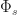 are irreducible (a basic fact from algebra), we get the following.
are irreducible (a basic fact from algebra), we get the following.
(4) For all 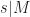 with
with 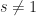 , the cyclotomic polynomial
, the cyclotomic polynomial 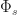 must divide at least one of
must divide at least one of  and
and 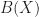 (possibly both).
(possibly both).
The question of interest is how these cyclotomic divisors are split between  and
and 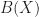 . Let
. Let 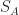 be the set of prime powers
be the set of prime powers 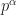 such that the corresponding cyclotomic polynomial
such that the corresponding cyclotomic polynomial 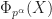 divides
divides  . In 1998, Coven and Meyerowitz proposed the following tiling conditions.
. In 1998, Coven and Meyerowitz proposed the following tiling conditions.
(T1) 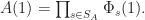
(T2) If 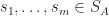 are powers of distinct primes1, then
are powers of distinct primes1, then 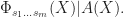
Theorem (Coven-Meyerowitz). Let 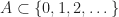 be finite.
be finite.
(i) If  satisfies (T1) and (T2), then
satisfies (T1) and (T2), then  tiles the integers by translations.
tiles the integers by translations.
(ii) If  tiles the integers by translations, then (T1) holds.
tiles the integers by translations, then (T1) holds.
(iii) If  tiles the integers by translations and
tiles the integers by translations and  has at most two distinct prime factors, then (T2) holds.
has at most two distinct prime factors, then (T2) holds.
We do not know whether (T2) must hold for all finite sets that tile the integers. The statement that this must be true has become known as the Coven-Meyerowitz conjecture, even though Coven and Meyerowitz did not actually conjecture this in their paper2. This is considered to be the main conjecture in the theory of integer tilings in 1 dimension. The problem turned out to be very difficult and there was very little progress on it until my recent work with Itay Londner – but more on that in future posts.
The (T1) and (T2) conditions may look technical and unintuitive at first – I remember that this was my impression the first time I saw them. So, let’s try to unpack them a bit and figure out what is going on.
It’s relatively easy to see that if  tiles the integers, then (T1) holds. Indeed, suppose that
tiles the integers, then (T1) holds. Indeed, suppose that  for some
for some 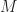 and
and 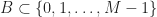 . Let
. Let 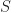 be the set of all prime powers dividing
be the set of all prime powers dividing 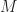 . By (4), we have
. By (4), we have 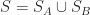 . Also, by (3) we have
. Also, by (3) we have 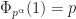 . Therefore
. Therefore

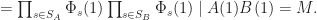
It follows that we must have equality at each step, and in particular (T1) holds for both  and
and 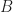 . (Additionally, this proves that
. (Additionally, this proves that 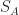 and
and 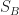 are disjoint.) I think of it as a “counting condition”, in the following sense: if
are disjoint.) I think of it as a “counting condition”, in the following sense: if  is to tile the integers, its mask polynomial cannot afford to have irreducible divisors
is to tile the integers, its mask polynomial cannot afford to have irreducible divisors  with
with  other than prime power cyclotomics, each with multiplicity 1. Otherwise, the tiling condition (1) fails because the cardinalities of
other than prime power cyclotomics, each with multiplicity 1. Otherwise, the tiling condition (1) fails because the cardinalities of  and
and 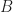 cannot match the tiling period.
cannot match the tiling period.
This is enough to prove that the 3-element set  (a modification of the earlier example) does not tile the integers. We have
(a modification of the earlier example) does not tile the integers. We have 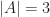 . If
. If  did tile the integers, there would be exactly one
did tile the integers, there would be exactly one 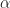 such that
such that  . Divisibility by prime power cyclotomics has a combinatorial interpretation in terms of equidistribution: if
. Divisibility by prime power cyclotomics has a combinatorial interpretation in terms of equidistribution: if 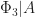 , then the elements of
, then the elements of  are equidistributed mod 3; if
are equidistributed mod 3; if 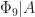 , then the elements of
, then the elements of  within each residue class mod 3 are equidistributed between the 3 available residue classes mod 9; and so on. In the given example,
within each residue class mod 3 are equidistributed between the 3 available residue classes mod 9; and so on. In the given example, 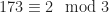 and
and  , so
, so  is not equidistributed mod 3. It cannot satisfy the higher order equidistribution condition, either, because each residue class mod 3 contains fewer than 3 elements of
is not equidistributed mod 3. It cannot satisfy the higher order equidistribution condition, either, because each residue class mod 3 contains fewer than 3 elements of  . Therefore, no tiling for this
. Therefore, no tiling for this  .
.
Going back to 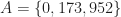 , can we use the Coven-Meyerowitz theorem to decide whether
, can we use the Coven-Meyerowitz theorem to decide whether  tiles the integers? Yes. First, observe that
tiles the integers? Yes. First, observe that 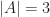 is a prime number, so that the (T2) condition is vacuous. It therefore suffices to check (T1). (This, and the extension to prime powers, was already known to Newman.) We need to look at divisibility of
is a prime number, so that the (T2) condition is vacuous. It therefore suffices to check (T1). (This, and the extension to prime powers, was already known to Newman.) We need to look at divisibility of  by
by 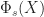 , where
, where  runs over powers of 3. Since
runs over powers of 3. Since  is a full set of residues modulo
is a full set of residues modulo 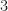 as pointed out earlier, we see that
as pointed out earlier, we see that  tiles the integers with period 3, this time with less wild guessing and a little bit more of a systematic method.
tiles the integers with period 3, this time with less wild guessing and a little bit more of a systematic method.
What about (T2), then? This is a deeper structural property that can be understood in several ways. One interpretation is in terms of equidistribution (possibly within residue classes). Suppose, for example, that 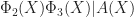 . Since 2 and 3 are powers of distinct primes, in order for
. Since 2 and 3 are powers of distinct primes, in order for  to satisfy (T2) we must also have
to satisfy (T2) we must also have 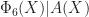 . This means that
. This means that
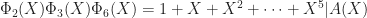 ,
,
so that  must be equidistributed mod 6. For example, the set
must be equidistributed mod 6. For example, the set 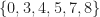 (a complete set of residues mod 6) satisfies (T2) and tiles the integers. On the other hand, if we let
(a complete set of residues mod 6) satisfies (T2) and tiles the integers. On the other hand, if we let 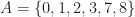 , then this set is equidistributed mod 2 and mod 3 (hence
, then this set is equidistributed mod 2 and mod 3 (hence 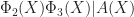 ), but is not equidistributed mod 6. Therefore (T2) fails, and by the Coven-Meyerowitz theorem for 2 prime factors,
), but is not equidistributed mod 6. Therefore (T2) fails, and by the Coven-Meyerowitz theorem for 2 prime factors,  does not tile the integers. Of course, for this particular set, we could also see it by inspection (there is no way to cover the numbers 4,5,6 by a translate
does not tile the integers. Of course, for this particular set, we could also see it by inspection (there is no way to cover the numbers 4,5,6 by a translate 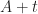 not overlapping with
not overlapping with  ). However, it’s easy to make up examples that look more complicated, but are actually equivalent once you know what to look for. For instance,
). However, it’s easy to make up examples that look more complicated, but are actually equivalent once you know what to look for. For instance,  might be less obvious, but has the same set of residues mod 6 as
might be less obvious, but has the same set of residues mod 6 as  , and does not tile the integers for the same reason.
, and does not tile the integers for the same reason.
Another way to understand (T2) that turned out to be rather important in our work is in terms of “standard” tiling complements. Suppose that  satisfies (T1) and (T2). To prove that
satisfies (T1) and (T2). To prove that  must then tile the integers, Coven and Meyerowitz constructed a tiling with period
must then tile the integers, Coven and Meyerowitz constructed a tiling with period 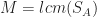 and an explicit tiling complement
and an explicit tiling complement 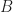 that depends only on the prime power cyclotomic divisors of
that depends only on the prime power cyclotomic divisors of  . (This happens in the proof of Theorem A in their paper.) Londner and I prove in Section 4.1 of our first paper that having this standard tiling complement is in fact equivalent to (T2). Therefore, to prove that (T2) holds for all finite tiles, it suffices to prove the following: whenever
. (This happens in the proof of Theorem A in their paper.) Londner and I prove in Section 4.1 of our first paper that having this standard tiling complement is in fact equivalent to (T2). Therefore, to prove that (T2) holds for all finite tiles, it suffices to prove the following: whenever  tiles the integers, it also admits a tiling
tiles the integers, it also admits a tiling 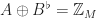 , where
, where 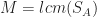 and
and 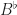 is the standard tiling complement for
is the standard tiling complement for  constructed according to the Coven-Meyerowitz algorithm.
constructed according to the Coven-Meyerowitz algorithm.
For the sets we considered so far, the standard tiling complements are very simple. If  is a 3-element set with
is a 3-element set with 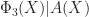 , we have
, we have 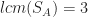 and
and 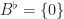 . Similarly, if
. Similarly, if  is a 6-element set with
is a 6-element set with 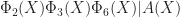 , we have
, we have  and
and 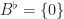 . Note that the set may have other tiling complements: for instance, if
. Note that the set may have other tiling complements: for instance, if  , then there is also a tiling of minimal period 12, namely
, then there is also a tiling of minimal period 12, namely 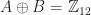 with
with  . (But we still have the standard tiling of period 3.)
. (But we still have the standard tiling of period 3.)
In general, we get 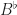 by “filling in” the cyclotomic divisors that might be missing from
by “filling in” the cyclotomic divisors that might be missing from  . Let’s say for example that
. Let’s say for example that 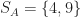 , and assume also that
, and assume also that  satisfies (T2). Since
satisfies (T2). Since 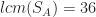 , we will try to construct a tiling
, we will try to construct a tiling  . Note that 2 and 3 are not included in
. Note that 2 and 3 are not included in 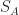 , so that by (4), we must have
, so that by (4), we must have 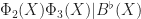 . If we just try
. If we just try
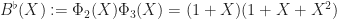
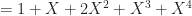 ,
,
there are two problems with that. First of all, this is not a mask polynomial of a set (because the coefficient of 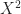 is 2). Second, we need all cyclotomic polynomials
is 2). Second, we need all cyclotomic polynomials 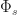 with
with 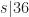 and
and 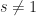 to divide one of
to divide one of  and
and 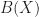 , and our assumptions on
, and our assumptions on  only guarantee that
only guarantee that 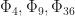 divide
divide  . (It is possible that
. (It is possible that  also has some of the other “mixed” cyclotomic divisors, but we do not know that.) So, we will assign preemptively all of the remaining cyclotomic divisors to
also has some of the other “mixed” cyclotomic divisors, but we do not know that.) So, we will assign preemptively all of the remaining cyclotomic divisors to 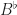 . We can do that by letting
. We can do that by letting
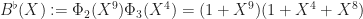
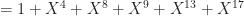 ,
,
which fixes both problems. (If you’ve read everything here so far, verifying this is a good exercise.) This produces a tiling complement 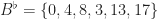 which is both highly structured (a sumset of the arithmetic progressions
which is both highly structured (a sumset of the arithmetic progressions  and
and  ) and determined entirely by the prime power cyclotomic divisors of
) and determined entirely by the prime power cyclotomic divisors of  .
.
More math next time, but this post would not be complete without some speculation.
Do I think that the conjecture is true? I honestly don’t know, and there are good reasons to expect either outcome. On the negative side, integer tilings can get rather complicated very quickly. There is already a huge jump in difficulty when passing from the 2-prime case to the simplest genuinely 3-prime tilings (the Coven-Meyerowitz paper has 12 pages; my papers with Londner add up to about 200). Beyond that, there be dragons nobody really knows. Wide-sweeping conjectures about tiling and group factorization do not have a good track record of being true without further restrictions, see for example Keller’s conjecture on face sharing in cube tilings, Fuglede’s spectral set conjecture, the conjectures of Hajós and Tijdeman on factorization of finite abelian groups, or, more recently, the periodic tiling conjecture. A general philosophy regarding questions of this type is mentioned in this Quanta Magazine article on the unit conjecture in algebra, which was eventually disproved: “At the time, there was little evidence either way. If anything, there was a philosophical reason to disbelieve the conjectures: As the mathematician Mikhael Gromov is said to have observed, the menagerie of groups is so diverse that any sweeping, universal statement about groups is almost always false, unless there’s some obvious reason why it should be true.” Tilings, too, can be quite diverse and there is a good chance that we do not understand yet the full complexity of the problem, so that situation here may well be similar3.
On the other hand, the Coven-Meyerowitz conjecture does not try to claim anything about tiling and abelian groups in general. It is, specifically, a statement about tilings of the integers, and that makes it a conjecture in number theory at least as much as one in algebra. In number theory, of course, heuristic considerations are quite different. “Serious” conjectures are generally expected, and often confirmed in the end, to be true unless there is some clear reason why this should not be the case.
So, ultimately, I think it will be a tug of war between these two sides of the conjecture. If the resolution turns out to depend on its algebraic aspects, it will likely be negative. If on the other hand the number-theoretic considerations prevail, then the conjecture should be expected to be true, although probably very difficult to prove. Based on my experience (for example, my work with Londner depends very strongly on the fact that we are in a number-theoretic setting), I expect that number theory is more likely to win here. I don’t consider it anywhere close to guaranteed, though, so I’d give it the odds of maybe 55-60%.
If you’d like to tell me what you think, the comments here are closed and will stay closed, but I’m on Twitter and Mastodon (see the sidebar for links), and if that format is not sufficient then I also have a Discord server for math discussions (ask me about getting an invite).
1 Note that 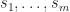 should be powers of distinct primes, and not just distinct prime powers. For example, if we assume that
should be powers of distinct primes, and not just distinct prime powers. For example, if we assume that 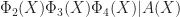 , then (T2) says that
, then (T2) says that 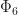 and
and  also divide
also divide  , but it does not say anything about
, but it does not say anything about 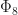 .
.
2 This is common practice in mathematics. For example, the Kakeya conjecture (a subset of 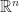 that contains a unit line segment in every direction must have Hausdorff dimension
that contains a unit line segment in every direction must have Hausdorff dimension 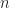 ) was named after Sōichi Kakeya, who did not conjecture any such thing. The question that he did ask concerned rotating a needle in the plane, and said nothing about either higher-dimensional spaces or the Hausdorff dimension.
) was named after Sōichi Kakeya, who did not conjecture any such thing. The question that he did ask concerned rotating a needle in the plane, and said nothing about either higher-dimensional spaces or the Hausdorff dimension.
3 For the same reasons, I had not expected the periodic tiling conjecture to be true. I said so when I was interviewed for the Quanta article about it. I was probably not alone in it, either. Instead, Quanta chose to publish a straightforward “mathematicians believed it was true” story and to quote me only on something technical.
such that
for some positive integer
. This means that
for some integer
; if
is relatively prime to
, we say that
is a primitive
-th root of unity, meaning that
is not a
-th root of unity for any
.
are roots of unity?







